Diffusion Lengths and Dimensionless Numbers
Diffusion Length
Diffusion Length
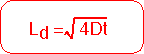
The diffusion length is the characteristic length scale for diffusion problems. It increases as the square root of the time. For semi-infinite regions, the solution looks the same for all times if the length is scaled by the appropriate diffusion constant for that time.
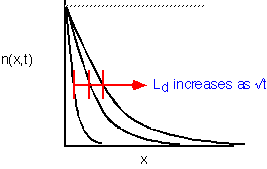
However, for real finite systems (like chemical vapor deposition reactors) the behavior of solutions changes qualitatively depending on how large the system is in comparison to the diffusion length.
If the diffusion length is much longer than the system size, the profiles of concentration must be essentially linear, and are independent of time (if diffusion is the only thing happening). A change in one part of the reactor is reflected throughout the reactor in a diffusion time (L2/4D). Note that the relevant time used to find the diffusion length will often be the residence time of gases in the reactor. As we'll discuss below, in this case fluid velocity is generally not important: diffusion dominates transport.
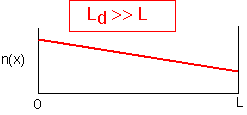
If the diffusion length is much shorter than the system size, concentrations can differ drastically from one part of the reactor to another. Gradients can be very large, and concentrations are highly time-dependent. Large changes in concentration in one region in the reactor will have no effect on other regions if the time involved is short enough that the diffusion length is small.
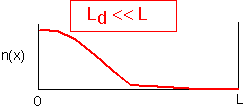
Chemical Engineers and Dimensionless Numbers
The diffusion length is our first introduction into a characteristic scale for a problem. Chemical engineers like to divide a characteristic length (like the reactor size, for example) by such a characteristic scale for a physical process, to obtain a dimensionless number. Instead of asking whether the length scale is large or small relative to the system, they ask the entirely equivalent question, is the relevant dimensionless number large or small compared to 1?
This approach is mathematically fine, but I personally find it very hard to remember! It is much easier to keep things straight when a physical quantity (like a length or time) is calculated and compared to the relevant parameter for your system. Therefore in this tutorial we'll usually use length and time scales, but we'll try to remember to translate them into Chemical Engineerese to help the reader access the technical literature.
An Example: The Peclet Number
An important example is the ratio between the system length and the diffusion length, typically calculated with the time set to the residence time (the average time gases are in the reactor). In order to avoid having square roots in the calculation, it is traditional to calculate the SQUARE of this ratio (with a constant factor): the Peclet number Pe, which works out to be the product of system length and fluid velocity, divided by diffusivity. If Pe >>1, large gradients can exist. If Pe << 1, diffusion dominates transport and things are linear.
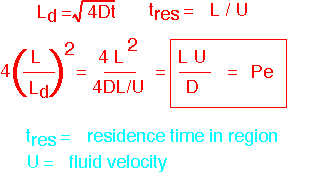
Pe can also be seen as the ratio of convective flux to diffusion flux if the velocity is constant and concentration is linear. The flux ratio is a useful view when you're calculating things like deposition rates, but it is harder to visualize.
Thiele Diffusion
Let's consider the case where the Peclet number is much less than 1 -- that is, the diffusion length is much longer than the system size. In this case, all transport is dominated by diffusion: convection is insignificant within the chamber. If deposition (or any other reaction) occurs at the surface, there is a loss of species to the wall. Thus we must consider simultaneous transport by diffusion and loss by deposition, as shown below for the case of a long, thin region where concentration is approximately constant in the y-direction and we consider only transport in the x-direction. This relatively simple situation is actually of practical relevance, for example in a single-wafer reactor at low pressures (and low molar flows -- more later) or transport in between wafers in a tube furnace. This problem was originally studied in connection with catalysis in porous media, in which the consumption of species occurs not through deposition but through conversion into products.
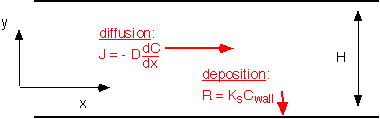
If we balance the moles entering and leaving a control volume dx wide we find:
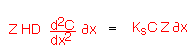
...from which we find the transport equation:
Solutions in one dimension are exponentials:
with x scaled by the Thiele length:

Naturally, we could also define the dimensionless Thiele modulus, the ratio of the system size to the Thiele length:

We can see how transport scales: larger separation between the surfaces encourages transport; and at lower pressures D increases, so if the reaction rate constant stays the same, the characteristic length increases (low-pressure or LPCVD).
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
