Simple Flow #2: Poiseuille / Couette Flow
If we consider the case of flow in a pipe or channel when Re is low BUT after the flow has been in the pipe for a distance much longer than the entry length, the fluid velocity will vary with radial position. The velocity must be zero exactly at the walls, and viscosity causes the velocity to be small in the vicinity of the walls. Therefore the flow in the center is actually faster for the same volumetric flow.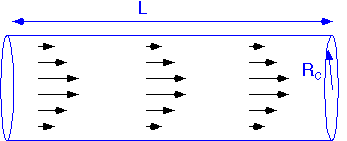
In the case of a cylindrical pipe with flow along the axis the velocity distribution is a simple quadratic, known as Hagen-Poiseuille or simply Poiseuille flow. A residence time and volumetric flow can again be defined in terms of the average velocity, but in this case the residence time is an average: streamlines near the center spend less time in the channel, and streamlines near the walls have very long actual residence times.
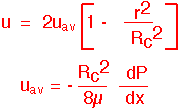
A similar treatment may be made of a channel "short" in one direction, which can thus be treated as flow between infinite parallel plates. Again action of viscous diffusion of momentum from the walls into the stream will cause the flow to become "fully developed" after a sufficiently long distance from the entrance.
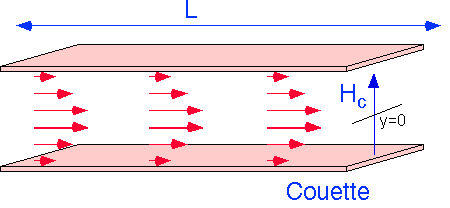
The distribution of velocity is quadratic with y-position.
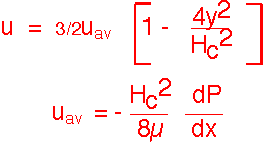
When large pressure differences exist across a long pipe (so that Re stays fairly small) one can integrate the Poiseuille formula to find the molar flow through the pipe (which of course is the same at all locations along the pipe in steady state). The expression is given below in terms of the input pressure, output pressure, length of the pipe L, and average pressure.
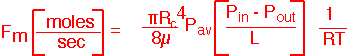
Note that the flow is very strongly dependent on pipe radius (the fourth power). In Couette flow the dependence is cubic on the separation of plates -- still very sensitive!
These fully-developed flows are often relevant in the pipes and channels that manage gas flow in CVD systems. In particular, it is often important to examine the pressure drop in gas supply piping. The integral formulation for Poiseuille flow as given above can be employed for this purpose, as long as the Reynolds number on pipe diameter is reasonably small -- up to a few hundred.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
