Simple Flow #1: Plug Flow
Two extremely simple flow configurations, valid for simple channels and small values of Re, can provide the basis for a lot of simple approximations for real transport. We will first examine how the simplest approximation to flow can be combined with our previous results on transport by diffusion to provide considerable insight into the operation of realistic reactor configurations. The first is plug flow: the velocity and direction of flow are constant everywhere in the system. Amazingly, such a simple flow is a fair approximation to actual flow in a simple channel or pipe when the Reynolds numbers (in this case, based on the pipe diameter D) are small, and when the distance from the entrance to the channel is small compared to the Entry Length, Le.
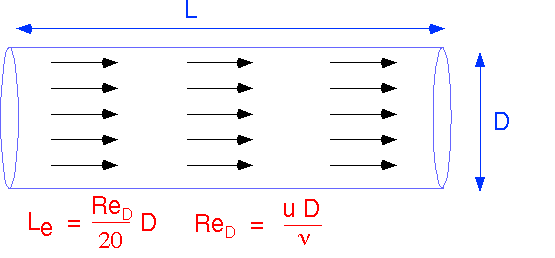
Plug flow allows us to define an unambiguous residence time which is the same for every streamline, since velocity is constant and the channel length is the same for all streamlines . The velocity U can be expressed in terms of the volumetric flow F and cross-sectional area A. If we ignore temperature differences (often OK) F in cc/second can be found easily from the molar flow in sccm.
Let's look at an example: a cubical chamber with a volume of 10 liters at ambient temperature, and total flow of 2 standard liters per minute (2000 sccm). At atmospheric pressure the gas in in the chamber for several minutes; at 1 Torr the corresponding time is less than 1 second. Again we see that pressure changes often encountered in CVD lead to tremendous changes in volumetric flow, velocity and residence time for the same molar flow.

A Plug Flow Reactor
Plug flow is an extremely simple tool, but we're going to put it to use anyway. Consider a simple rectangular reactor which has a gas inlet on one side, an exhaust on the other, and deposition on the top and bottom walls (and the sample, resting on the bottom surface):

To study this reactor we first need to define some notation for the dimensions and coordinates.
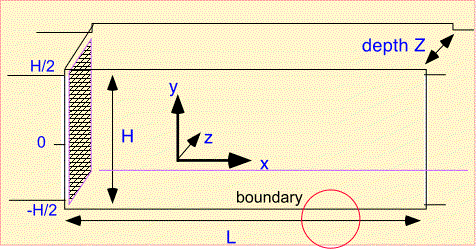
We make a key approximation, often useful in CVD:
- in the direction of flow (x) we only need to include convection in transport
- perpendicular to the direction of flow (y) only diffusion is important.
Finally, to fully define the problem we need to understand the boundary conditions. At the left edge the concentration is fixed as the amount of precursor in the incoming gas stream. On the top and bottom we need to account for consumption of the precursor in the growing film...

For simplicity we assume the top and bottom boundaries are identical. The boundary condition we need to use is somewhat complex, but often encountered in CVD and thus well worth examining. Recall that very near the surface only diffusion is active in transporting molecules. The diffusive flux to the surface must supply all the precursor which is incorporated into the film. The diffusive flux is the product of the gradient in concentration, dn/dy [where n is the density of molecules of interest], with the diffusivity D. The rate of consumption of molecules in the film is the surface reaction rate constant multiplied by the surface concentration (assuming simple first-order surface reaction). We set the two equal at the surface (shown in red) and obtain a relation between the concentration and the gradient at the surface. Note that this is the same as saying that the concentration goes to zero at an artificial boundary (D/Ks) beyond the actual boundary.
Finally, we use a simple trick: we travel along with the gas. This is easy because the velocity is constant everywhere. The concentration as a function of x and y is exactly the same as the concentration encountered in a stationary slice of gas as a function of position y and time t, if we let t be the "streamtime" tst = x/u.

Solving the (x,y) problem is thus the same as the problem we've already examined: the concentration in a one-dimensional slice of gas as a function of time, with transport due to diffusion within the gas.
Pay No Attention to the Math Behind The Curtain
Here we have to plunge into some rather dull algebra -- but if you can bear with the process, we'll try to expose the simplicity hidden in the special cases...
First recall the general solution to the one-dimensional diffusion equation:

When applied to our problem, we can simplify this ugly summation quite a bit right off the bat. Since the boundary conditions are the same at y = H/2 and y=-H/2, only the cosine terms can match the boundary conditions. The possible solutions must have the form:

Our problem is now to find the values of the unknown coeffients a and ⍵. In order to accomplish this, we apply the detailed boundary condition relating the flux and gradient at the surface to our general expression for concentration (and by differentiation under the summation sign, gradient as well):
The result is a rather nasty transcendental equation, with no obvious analytic solutions.

However, if we look at the equation graphically we can obtain insight into some useful approximations. In the figure below we have shown a graph of the left hand side (black) and the right hand side (red) of the boundary equation, graphed as a function of ⍵. Each point where these two graphs intersect is a solution of the boundary equation and thus an allowed value of ⍵.
Since the LHS contains a tangent term which has poles (infinite values) periodically, there must be an intersection near each of these poles no matter what the values of K and D. The poles of tan(x) occur at (mπ/2) for odd m-- but since w in the argument occurs in a square root, when plotted against ⍵ the poles go as m2 -- that is, they get farther and farther apart as m grows.

We can further simplify the problem by recognizing two limiting cases: either ⍵o is very near to 0, or it is close to the first pole of the tangent function. By substituting the value of the pole, proportional to (D/H2) in the right-hand side, we see that these two cases are equivalent to asking whether the ratio KsH/D is large or small.
In the first case, the RHS is small and ⍵o is nearly zero. We can approximate the tangent with its argument and obtain an approximation for ⍵o as:

It is interesting to note that this value is closely related to the "species consumption lifetime" we defined in our study of a zero-dimensional reactor. The factor of 2 just arises from the fact that in this case both the top and bottom surfaces of the region of interest are allowed to consume species.
In the second case, the RHS is large, and ⍵o can essentially be set equal to the position of the zero of the tangent function.

What Does It All Mean? (in 3 easy steps)
What the heck is KsH/D?
EASY ANSWER: the Damkohler number (remember what we said about chemical engineers?)
USEFUL ANSWER:
For a surface concentration of n, consumption of stuff at the surface = Ksn.
Characteristic diffusion flux for concentrations n over a region of size H = D dn/dx = Dn/H if the concentration is just linear. We therefore find:

The Damkohler number is the ratio of consumption at the surface to diffusion. When it is large, species are consumed more rapidly than they can diffuse to the surface, and we expect the surface concentration to fall relative to the rest of the chamber. When it is small, the reaction rate is slow and diffusion maintains concentration nearly constant.
What does the case KsH/D<< 1 mean?
Diffusion much more rapid than consumption => concentration is uniform in y; diffusion has no effect; the deposition is surface limited. Recall that in the case of the zero-D reactor we denoted the situation as surface-limited when the residence time was much shorter than the consumption lifetime. Here the diffusion time across the region, H2/4D, plays the role of the residence time; the Dahmkohler number can also be seen as the ratio of "residence time"/consumption time (H/Ks).

This is a "zero D" reactor stretched out in space by the streamtime transformation t => ux. The deposition rate (purple) falls off exponentially with characteristic length Utcon/2; the concentration (green) is nearly uniform in y and decreases as we proceed to the right (increasing x).
What does the case KsH/D>> 1 mean?
Consumption at surface is so rapid that for practical purposes n=0 at surface. After short entry length the concentration n(y) is a cosine (green at right) ; rate (purple at right) falls exponentially with length = Utdiff where tdiff= H2/D. Note that the rate here is set not by the surface concentration but by the gradient near the surface and thus the flux to it.

This is like a zero-D reactor in the transport-limited regime, save that we must use the diffusion time in place of the simple residence time.
Let's review what we just did:
- we estimated the concentration of species assuming simple plug flow along a channel and diffusion perpendicular to the flow, with "first-order" surface reaction (deposition rate and thus species consumption proportional to surface concentration)
- we arrived at a general solution consisting of an infinite sum of terms like (cos my)exp(-mt); we argued that since m grows rapidly, only the first term is likely to be important in most cases
- we further argued that the value of m, and thus the rate at which species are depleted from the gas stream by deposition, will have two interesting limit cases
- a surface - limited case where concentration is nearly uniform in y, and the characteristic length for depletion is controlled by the ratio of chamber height (amount of stuff) to surface rate constant (consumption of stuff), multiplied by the velocity which moves everything along the chamber
- a transport - limited case, where concentration is nearly zero at the surfaces and the characteristic length is controlled by the diffusion time in the chamber, H2/D, multiplied again by the velocity.
If we include our earlier treatment of the diffusion - only (Thiele) case we can summarize the various ways that deposition can occur along a channel, with first-order surface reactions:
Transport by diffusion only:
diffusion flux >> convection flux
D/L >> U

Convection in x, fast diffusion in y:
fast diffusion vs. convection in x
D/L >> U
fast diffusion in y
Ks << D/H

Convection in x, fast reaction at surface:
fast diffusion vs. convection in x
D/L >> U
slow diffusion in y
Ks >> D/H

What are the effects of pressure?
We have shown that as pressure varies, flow velocities change tremendously. Does any of this laminar flow stuff mean anything? Do the limiting cases we've studied ever arise? To answer these questions let's examine the effect of pressure on three important parameters...
The Reynolds Number:

So if a flow was laminar at atmospheric pressure, it is laminar at 1 Torr. Huge changes in pressure don't significantly change flow configurations (as long as we remain in true fluid flow -- see our discussion of Knudsen flow).
The Peclet Number:

So if diffusion was more important than convection at atmospheric pressure, it remains so at low pressure.
So far pressure looks like a seriously wimpy parameter. However, once we introduce surface reactions and start examining depletion we get a different answer...
Depletion Length:
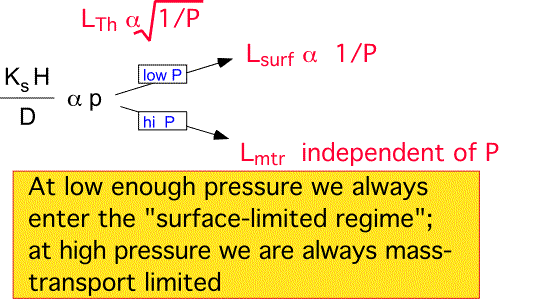
Low pressures encourage long depletion lengths, either due to diffusion if convection is negligible, or due to the increased convective velocity relative to a fixed rate of surface reactions. At high pressures the mass-transfer-limited regime is always reached; here the depletion length becomes independent of pressure, since both the velocity and the diffusivity scale the same way with pressure. Since deposition uniformity is improved by a slow depletion of species, low pressure is an important weapon in the commercial arsenal. However, pressure reduction also reduces the absolute deposition rate through the decrease in density; uniformity and throughput must be traded off to reach a practical industrial process.
An Example
Consider our previous cubical chamber with volume of 10 liters and thus a linear dimension of about 22 cm, and a gas flow of 2 standard liters/minute (2000 sccm), ignoring any thermal expansion...

The careful reader will note that the assumption of plug flow becomes somewhat questionable in those cases where the Reynolds numbers are small and true mass transport limitation occurs. A more precise calculation will assume Poiseuille or Couette flow, at a considerable increase in mathematical complexity with little improvement in physical insight.
SUMMARY of this very long page:
In this long but hopefully fruitful discussion we've used the simplest possible combination of convection and diffusion to classify reactors based on dominance of different transport mechanisms: diffusion or convection. We've also found that pressure has a modest effect on flow and the balance between convection and diffusion, but a huge effect on the relation between transport and deposition.
While the detailed quantitative results we obtained are rather limited in applicability, the classification approach is generally useful. In fact, as we'll see shortly, much more sophisticated treatments including the formation of velocity and thermal boundary layers near a surface don't affect the general results we've obtained very much, because in typical gases the diffusivities of mass, momentum, and energy are roughly equal. Thus, when you're faced with a more complex reactor configuration, it pays to start the thought process by treating the reactor as a box and figuring out which category in our scheme it fits best.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
