Boundary Layers and More General Flows
The two flows we've studied are actually the two extreme cases of flow in a "duct" or chamber, as shown below: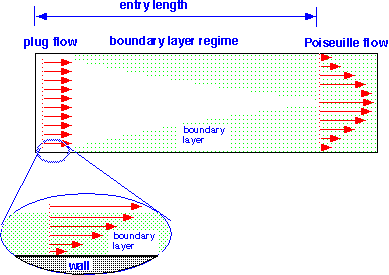
In the "plug flow" regime, the real flow configuration has nearly constant velocity in most of the chamber, with a relatively thin "boundary layer" in which the gas or fluid is strongly affected by viscous drag from the walls. In plug flow the boundary layer is so small that we can ignore it to first order -- that is, the flow is "inviscid". In the Poiseuille regime, the two boundary layers have grown so much that they no longer exist as distinct regions, but have merged to give a smooth continuous variation in velocity.
In the intermediate region, we can treat the flow as taking place in two distinct regions: a boundary layer with low velocity, whose thickness we need to determine, and a "free stream" region outside the boundary where velocity (and other parameters such as concentration) are relatively fixed.
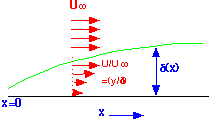
The boundary layer formation is the result of diffusion of momentum from the wall into the stream. To first order, we can treat this problem just as we did the plug-flow reactor, by allowing diffusion to proceed perpendicular to the streamlines, and taking the gas flow velocity into account through a streamtime transformation t => x/U. We use the kinematic viscosity as the diffusivity of momentum.
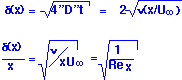
Note that the result can be expressed in terms of the Reynolds number -- as we noted, Re is a measure of the relative size of the momentum diffusion length and the system. Note also that the boundary layer grows as the square root of the distance downstream.
In most gases we're interested in, the kinematic viscosity and the mass diffusivity have very similar values -- in Chemical Engineerese, the Schmidt number is near 1. When this is the case, a "mass diffusion" boundar layer will form near a surface where consumption is occurring [i.e. where a film is being deposited] in pretty much the same way that the velocity boundary layer forms. For the sort of factor-of-two accuracy that our simple models can expect to obtain, one can get away with ignoring the existence of the velocity boundary layer altogether, and just consider the depletion of precursors near the surface:
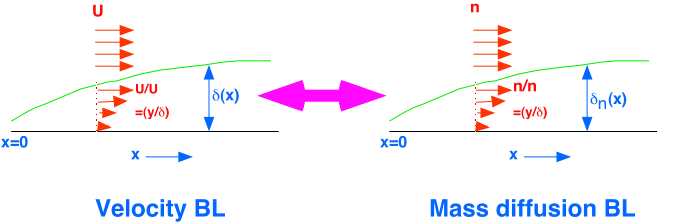
If we return to the ideas we introduced in our discussion of a plug flow reactor, we see that if we're in the surface limited regime we really don't care much, since transport has little effect on rate. In the mass-transport-limited regime, whether we need to consider the boundary layer depends on whether the thickness of the boundary layer is small with respect to the chamber size (equivalently, whether we can get away with considering only the first term in the diffusion equation solution). If the boundary is thin, then one can effectively divide the chamber into a central region with constant concentration and a boundary region across which the concentration falls in a roughly linear fashion, such that the flux to the surface goes inversely as the square root of the thickness of the boundary layer.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
