Ion Flux to Surfaces: The Bohm Velocity
We've mentioned several times that ions from the plasma bombard surfaces. How many ions are there? To answer this question we need to look in more detail at the sheath region.
At the Sheath Edge: Ions Falling In
As the ions enter the sheath, they are accelerated by the field and their density must decrease to maintain a constant flux. If this decrease is too fast, the ion density will fall off before the electrons (which diffuse a bit into the region of positive potential) vanish, leading to a net negative charge, which would then increase the ion velocity. The stable solution must occur when the ions entering the sheath have enough initial velocity to ensure that the sheath remains positive. Let's examine this condition quantitatively. We'll first examine a collisionless sheath: that is, we assume that the ions can fall through the sheath region without colliding with a neutral molecule. Notation is defined below:
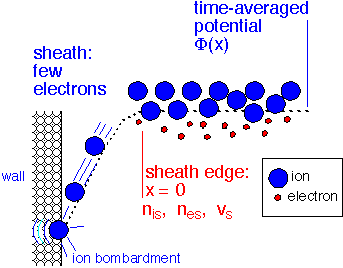
The ion flux is constant in the sheath (that is, we assume negligible ionization or recombination there). The flux of ions J = (density)*(velocity) must therefore be constant and equal to the flux at the sheath edge.
If the ions move without collision, their velocity in the sheath is determined by the requirement that the kinetic energy gained equal the change in potential relative to the sheath edge:
We can then obtain the density of ions as a function of the potential (which is an as-yet unspecified function of position) and the density and velocity at the sheath edge:
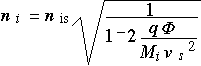
The electron density is obtained by assuming that the electrons move into the sheath region by diffusion: the concentration at any location is proportional to the energy at that location divided by the electron thermal energy kT:
In order to ensure that the sheath charge is always positive, we impose the condition that the ion density falls more slowly than the electron density at the sheath edge (and everywhere else in the sheath):
The rate of change in the ion density is obtained by direct differentiation of our expression for density. The quantity in the radical is = 1 at the sheath edge, because the potential is zero there.
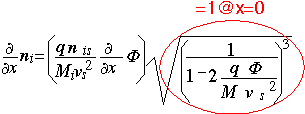
Similarly we obtain the rate of change of the electron density. Here the exponential term is = 1 at the sheath edge where the potential is zero.
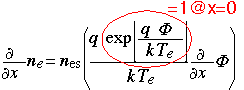
If we set the two terms equal, we find the minimum velocity allowed at the sheath edge: the Bohm velocity. Since the ion flux is continuous in the sheath, the ion flux to the wall is then the product of the Bohm velocity (which depends only on the electron temperature and the ion mass) and the plasma density at the sheath edge:
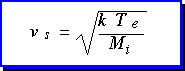
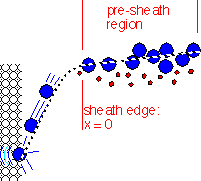
The finite Bohm velocity implies the existence of a pre-sheath region: a weak electric field penetrating into the plasma near the sheath edge, which accelerates the ions as they enter the "main" sheath. The potential change in the pre-sheath region is on the order of kTe -- that is, equal to the thermal energy of electrons.
What does this mean for plasmas of interest? Let's look at some numbers:
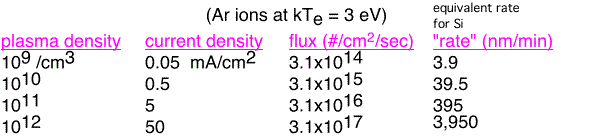
The ion current in deposition plasmas will vary from a few microamps to a few milliamps per square centimeter. If we multiply this by a typical ion energy of 100 volts or so, we find that a lot of power is dissipated as these ions strike the walls: e.g. in a high density (1011 electrons/cm3)plasma the power delivered to the substrate surface by ion bombardment is 0.5 W/cm2, or 150 Watts to a 200 mm wafer. Note that the equivalent rates can get very high in a high-density plasma: 395 nm/min is 4 microns/minute -- an adequate deposition rate for a single-wafer reactor. At high plasma density, ion fluxes can exceed deposition rate even in a high-deposition-rate reactor. We will find that this high ion flux has strong effects on the properties and topography of the deposited film when we study high-density plasma deposition.
In the case of a collisional sheath (more appropriate for many CVD processes at > 1 Torr), the sheath velocity is reduced relative to the Bohm velocity by the ratio of the ion mean free path to the Debye length. The Debye length is the characteristic length over which the plasma electrons screen an applied potential; numerically it is approximately
where the length is in cm, the electron temperature in volts (i.e. actually kT/q), and the density in number/cm3. For a 4 eV plasma with density of 1E10/cm3, the Debye length is 0.014 cm or 140 microns. The mean free path of ions is similar to the neutral mean free path.
Return to Tutorial Table of Contents
Book version of the CVD Tutorial
