Introduction to Wireless Links for Digital Communications
Part 1: Multiplexing, Modulation, and Link Budgets
Daniel M. Dobkin
January 2004
Introduction
This article is meant to provide an introduction to how a wireless
device (a radio) is used to move information between two locations.
We'll focus on the analog part of the problem: how waves move
around, how you sort out one wave from another, how to figure
out how far you can go and what can and can't be done. The actual
inner workings of the radios and antennas that do the job of converting
a signal to a wave and back again will be covered in a subsequent
missive.
Electromagnetic Waves
As soon as you see the word "electromagnetic", you'll
be waiting to see references to electric and magnetic fields.
If you've taken college courses on the subject, you'll be primed
(that's a math joke) for boldface letters B and H
for the magnetic stuff and E and D for the electrical
quantities, and memories of funky vector equations like A x (B
x C) = (A*C)B - (A*B)C will pop up. You're going to be disappointed
(hopefully the biggest disappointment you as a reader will experience
with this article). We will attempt to exclusively refer to the
four-vector potential A, composed of the conventional three-vector
potential A and the electrostatic potential f.
In this approach we follow Carver Mead's Collective
Electrodynamics (MIT Press, 2000), though perhaps less
dogmatically than Professor Mead. For example, we shall simply
adopt the use of retarded potentials (signals received at a distant
point come after they are transmitted) rather than agonizing over
the ideal symmetrical equations and the role of infinitely distant
objects in making time progress unidirectionally. (The reader
who has the time to worry about why they have time and why time
exists at all and why Einstein was wrong in thinking its progress
to be an illusion may with to consult Order
out of Chaos, by Prigogine and Stengers, in addition to
Mead and references therein, for a somewhat different viewpoint.
'Nuff said.)
|
All radio communications exploits a basic fact about
our world: a current in a location [1] induces a potential A
in a distant location [2]. The potential can in turn induce a
current at the distant location. The distant location feels the
current after a time dt = r/c, where r is the distance between
[1] and [2]. The magnitude of the induced potential decreases
as (1/r).
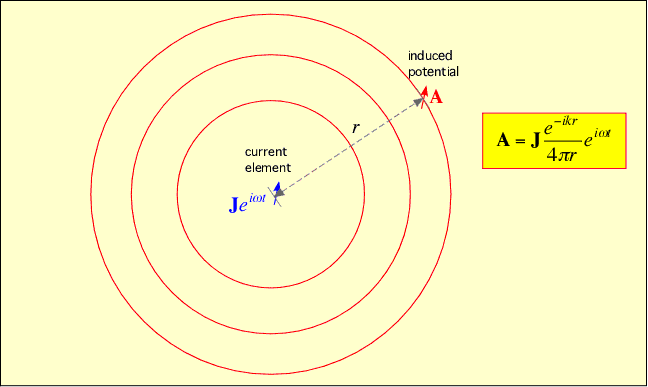
One could write A([2], t) = J([1], t-r/c), but in radio
engineering we almost always take everything, including currents,
to be harmonic: that is, we assume it has a time dependence like
J = cos(wt), or more generally, taking
into account the possibility that phases can change, J = exp(iwt) where the complex exponential is defined
as exp(ix) = cos(x) + i sin(x).
For convenient reference here we include a brief discussion
of complex exponentials.
|
 |
Multiplexing
In the real world, many simultaneous transmissions are occurring.
An antenna (i.e. at location [2]) doesn't just pick up what you're
looking for, but the total potentials due to all currents on its
light cone (all the points in the universe from which light would
reach the antenna at the time of interest). In order to actually
communicate, we somehow have to find the signal we are looking
for amongst all the other possible signals. A different way of
viewing the same problem is to say that many signals share the
same medium: we need to arrange for some kind of multiplexing
to allow all these signals to exist simultaneously while still
picking out the one we want. There are many methods of multiplexing:
- Frequency-division multiplexing: In this approach
we look only for signals with a given periodicity and shape.
To be more specific, we search only for signals which look very
nearly like cos(wt) (to within a phase
shift) for some particular value of the frequency f or w = 2pf. We
can do this because different frequencies of a sinusoidal signal
are orthogonal: their product averages to zero.
-
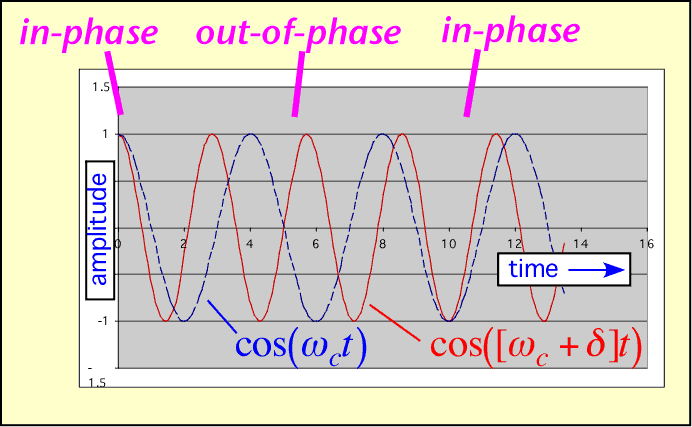
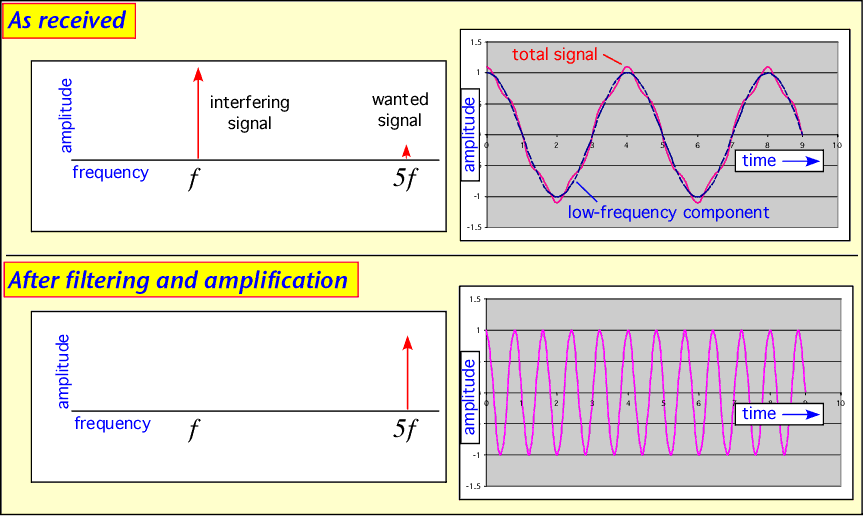
- Almost all radio communications depend on frequency-division
multiplexing at least partially; government regulations and available
technology make this the simplest and most powerful of all methods
of sharing the wireless medium. Using filtering the desired signal
can be extracted even when it is much smaller than other interfering
signals. (The example shown below is somewhat idealized, but
very high rejection of unwanted frequencies can be obtained if
the frequencies are well-separated.)
- Spatial multiplexing: If my transmitter is farther
from your receiver than the realistic range of the signals, then
you don't care what I send. We can use the same frequency without
interfering with each other. This is the principle behind spatial
multiplexing, also known as spatial frequency reuse. On a global
scale, the FCC can allow FM radio stations in distant cities
to use the same channels (though AM radio can be ducted by the
ionosphere and travel across continents, making reuse more difficult).
Locally, conventional cellular telephony depends on frequency
reuse to allow thousands of subscribers of a single provider
to talk simultaneously in a given metropolitan area. Note, however,
that some cellular telephony also employs code-division multiplexing,
described below. Wireless local area networks (WLANs), which
normally operate at very low power and thus fairly short range,
are another example of the use of spatial separation to allow
frequency reuse, though here there is no central coordination
and collisions may occur. Fortunately, WLAN's are not on all
the time, leading us to:
- Time-division multiplexing: if you listen when I talk,
and I extend the same courtesy to you, we can converse even though
we use the same airmass to transmit our pressure-wave signals.
Similarly, a single frequency and location can be shared without
interference by dividing the total time into intervals, and assigning
each transmitter to a unique interval. By listening at the correct
moment we acquire only the signal of interest, and can ignore
other signals in the wireless medium at the same frequency and
location. An important limitation is that the range over which
such a scheme can be efficiently employed is limited by the propagation
velocity of light: you may transmit at the start of your slot,
t=t1, but if by the time the signal gets to me at t=t1+r/c =t2
my slot has started, I will erroneously listen to your signal
rather than the one I'm trying to receive.
- Direction of arrival: By employing an antenna more
sophisticated than a mere slip of wire, I can choose to receive
only signals arriving from particular directions and reject the
others. (It turns out that such a choice also carries the benefit
of collecting more of the received signal, improving sensitivity.)
This trick allows users to transmit on the same frequency at
the same time to the same location and still be disentangled.
However, there are tradeoffs: directional antennas are larger
and more expensive than 'isotropic' antennas, and you need to
know what direction to point the antenna in. The most common
use of such an approach today is to implement long 'point-to-point'
connections between two very directional antennas spaced 10-50
km apart; the antenna's directivity is used to capture the tiny
signal of the distant transmitter while rejecting other users
of the same frequency.
- Code-division multiplexing: A person can hold a conversation
with another nearby person in a crowded room with many other
conversations taking place simultaneously, as long as the other
sounds don't drown the intended speaker out altogether, because
our brains can listen for a specific voice in the cacophony.
Similarly, we can arrange for a given transmission to be extracted
from many simultaneous transmissions on the same frequency band
at the same place if we code the desired transmission. A simple
method of doing so is to multiply the data we are sending by
a specific pseudorandom sequence, which is known to both
the transmitter and receiver. For example, let us imagine I wish
to send you a (+1). I multiply this data bit by my particular
sequence, in this case (1 -1 1 -1 ), and thus send you (1 -1
1 -1 ). At the same time, another user sends a data bit of (-1)
using their particular code (1 1 -1 -1 ), so their transmission
is (-1 -1 1 1 ). At the receiver, you receive the sum of the
two signals: (0 -2 2 0). Multplying this signal by the desired
code (1 -1 1 -1) and averaging the result gives (0+2+2+0)/4 =
1, the bit from the desired transmitter. Note that for this trick
to work, the different users need codes that are orthogonal
or nearly so: that is, two codes multiplied together and averaged
(correlated) must yield 0 or at least something small compared
to the desired data.
Information and Modulation
In order to send information over a carrier of a given frequency,
we must make a change in something: the amplitude, frequency,
or phase of the signal. When we do so we inevitably introduce
new frequency components into the signal's spectrum. To see why
this should be so, we need to think about how we determine how
much power a signal has at a given frequency. We multiply the
incoming signal by the desired signal, cos(wt),
and integrate. The average of the integral over some suitable
period is the amount of the signal at the desired (angular) frequency
w.
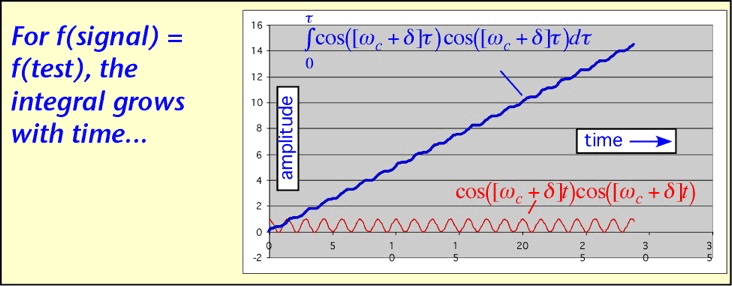
If the signal is a sinusoid with a different frequency from
the desired frequency, the integral will oscillate, averaging
to zero after a long time (differing frequencies are orthogonal):
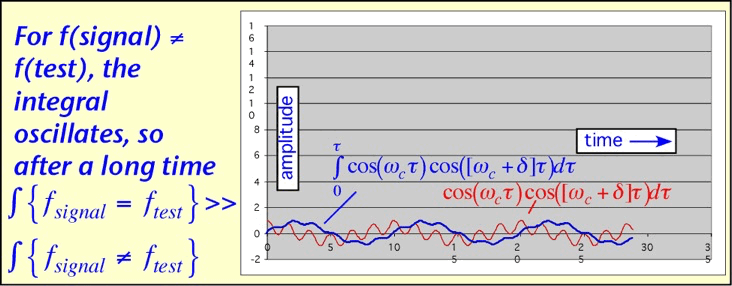
If we start with a simple sinusoid cos(wt)
and modulate it -- for example, change its amplitude slowly --
we will find that the average integral at a different frequency
is no longer necessarily 0.
If the test frequency is chosen so that the modulation turns
the signal on when e.g. the integrand is positive, and off when
the integrand is negative, the contributions will no longer cancel
over a long integration time: the modulated signal has acquired
a new frequency component corresponding to the sum or difference
of the original carrier frequency w
and the frequency of modulation d.
(The former is illustrated below.)
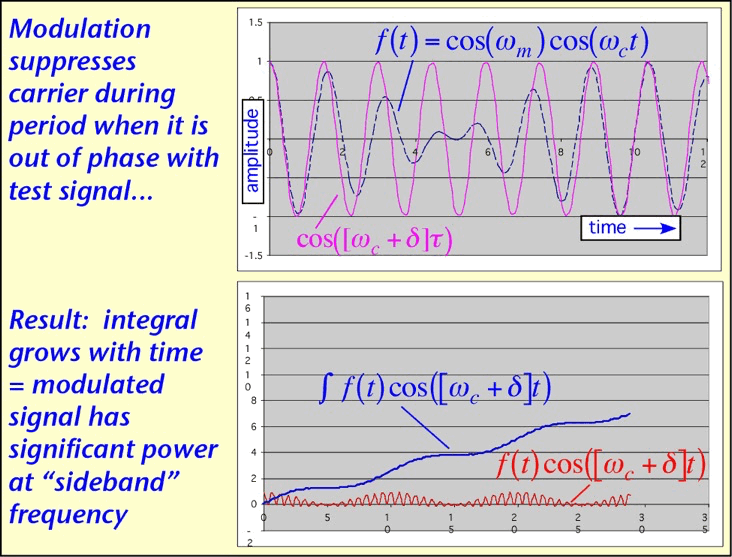
The resulting spectrum has components farther and farther away
from the initial carrier frequency when the rapidity of modulation
is increased (d is made larger): for
a given modulation scheme, higher data rate consumes more bandwidth.
It is almost always the case that bandwidth is limited, superficially
by regulatory requirements but more fundamentally by the requirement
to share with other radio users in the same physical location.
More sophisticated modulation schemes can be employed to send
more than one bit for each symbol, getting more data from
the same bandwidth, but at the cost of reduced immunity to noise.
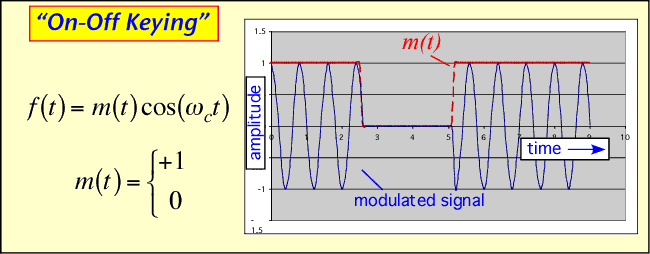
Let's examine a few examples. The simplest possible modulation
is the old Morse-code approach of turning the carrier on for a
1 and off for a 0; on-off keying. Here one bit is transmitted
per symbol. This approach is still widely employed in optical
fibers but is not often used in wireless communications.
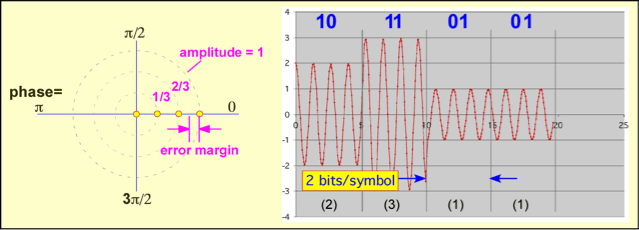
To send more data in the same spectrum we might use multiple
values of the amplitude instead of just ON or OFF: amplitude-shift
keying. Note we have depicted the signals here both as amplitude-vs-time
and amplitude-and-phase vs. time: the phase plane. The
problem with this scheme is that the amount of noise we can tolerate
before mistaking e.g. 11 for 10 is obviously less than in the
OOK scheme for the same peak power. This is shown as the error
margin in the phase plane diagram. Note that here, since we aren't
really explicitly keeping track of the phase, the yellow dots
could also be shown as circles without changing anything: the
error margin is also unchanged, as it is half the distance between
two adjacent circles irrespective of the angular location.
If we are willing to keep track of the RF phase, at the cost
of additional complexity we can get a much better noise margin
for the same data transmission rate. An example, shown below,
is the use of quaternary phase-shift keying, QPSK. We are
still able to send two bits for each symbol, but the error margin
is much larger than in the equivalent ASK case.
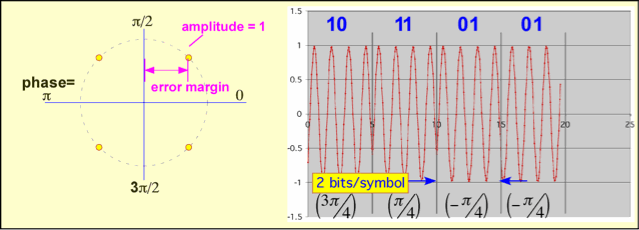
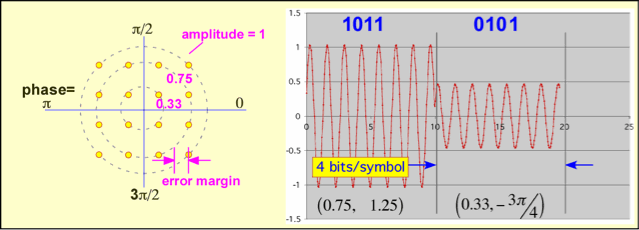
Both phase and amplitude can simultaneously be varied in quadrature
amplitude modulation (QAM). More bits can be send in each
symbol, but an unavoidable decrease in the tolerance for noise
results. Thus, QAM with many possible values works very well in
wired channels such as the coaxial cables employed (at least near
the customer's site) in digital cable TV, but may have a limited
range when employed in a wireless link.
Radio Link Overview
How much noise can we tolerate? The lower limit is set by the
thermodynamic fact that at a finite temperature, any degree of
freedom of a system with energy levels small compared to (kT)
is excited to contain an average energy of kT (where T is the
absolute temperature and k is Boltzmann's constant). Thus a resistor
of R ohms at room temperature has a mean square voltage between
its terminals of 4kTR per Hertz of bandwidth: in radio terms,
that's -174 dBm/Hz, where a dBm is a logarithmic
measure of power relative to one milliwatt: dBm = 10 log (P/ 1
mW). Real receivers have excess noise as well, measured by their
noise figure (also often quoted in dB). Thus, if our signal
is modulated at around 1 MHz (a million cycles per second), its
bandwidth will be somewhere around 1 MHz and the noise level in
the receiver is about (-174 + 10 log (1,000,000) ) = -114 dBm.
That's about 4 picoWatts (1 millionth of 1 millionth of a watt),
which doesn't seem like much, but remember that the amount of
energy received by the antenna falls off by the square of the
distance in empty space, and is likely to be even smaller if people,
trees, buildings, cars, and billboards for iPods get in the way.
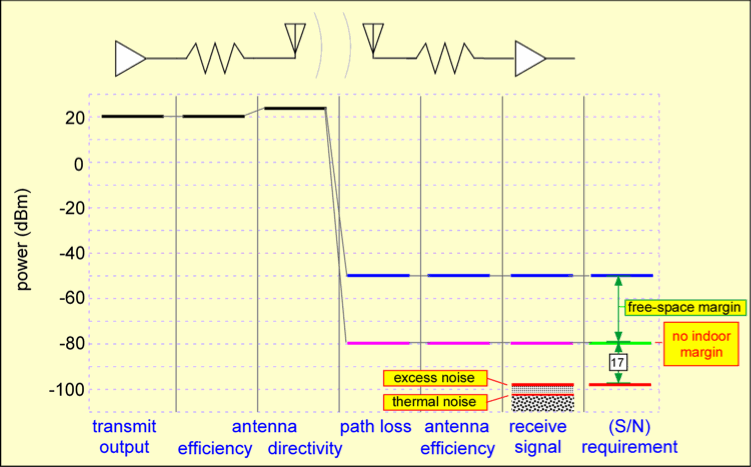
To examine the situation quantitively, we look at the starting
signal power at the transmitter and trace its path through the
antennas into the receiver. The resulting relationship between
signal and noise has to be good enough to support whatever modulation
we chose to try to use. An example of such a calculation is shown
below. The transmitted power is used effectively by having the
transmitting antenna 'point' at the receiving antenna (the directivity
of the antenna), but is decreased dramatically by the path loss:
the path loss in blue corresponds to free space, while than in
purple depicts the extra loss one might encounter indoors where
obstacles block and attenuate the signal. Meanwhile, the thermal
noise and the excess noise of the receiver raise the noise floor.
The ratio between the signal and noise, 17 dB in this example
for the 'indoor' path, represents the accuracy with which the
receiver can determine the amplitude and phase of the received
signal, and thus the number of bits that could be sent per symbol
before errors in determining which symbol was transmitted become
likely.
PART 2:
Antennas
For a more detailed discussion of these topics, see Dan's book, RF Engineering for Wireless Networks, Elsevier 2004.
RETURN TO COMMUNICATIONS INDEX